|
Introduction
|
|
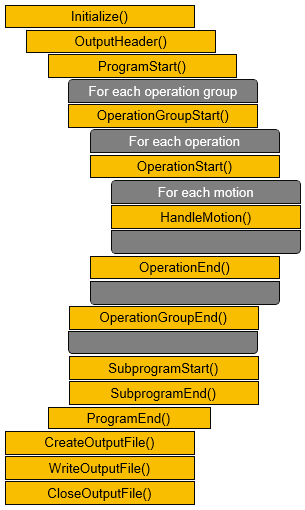
The picture below shows the simplified sequence of the standard function calls.
|
|
|
|
Each function has access to the dedicated object, for example an operation, but also to the controller, the electrical connected resources and the complete program.
|
|
Motion: A motion consists of one (linear or point-to-point) or two (circular) position objects (i.e. toolpath elements). Each position has its own coordinates, axis values, configuration, turn, etc. The motion can have events that effect before or after reaching the position. This means that the events are handled accordingly in the HandleMotion().
Operation: An operation normally contains several movements and combines them into a technological unit, for example a drilling point, welding seam or painting surface.
Operation group: An operation group encloses logical or technologically related operations in one group. The grouped operations can be manipulated together, as one entity.
|
|
|
Steps
|
|
|
|
1.1
|
In Visual Studio Code open the HelloWorld.py from the example plugin, that has been implemented during the preparation. If everything is set up correctly, the picture should look like this.
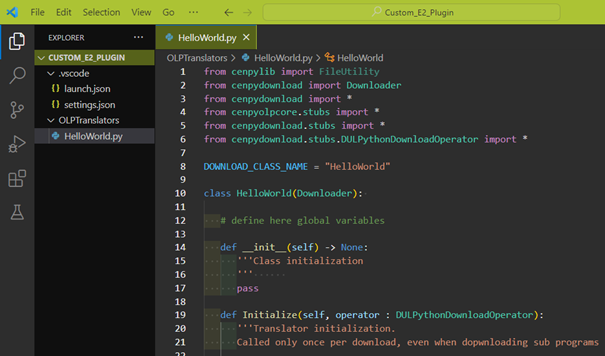
Trouble shooting:
 If the title bar is not green, please check if you selected the correct folder. If the title bar is not green, please check if you selected the correct folder.
 If the imports are underlined yellow, please select the Python interpreter from the FASTSUITE Edition 2 installation. If the imports are underlined yellow, please select the Python interpreter from the FASTSUITE Edition 2 installation.
Both issues are described in the Preparation page.
|
1.2
|
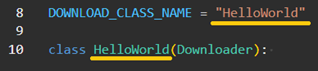
The name of the translator (file) and the Class names can be different. The file name is used and visible in the user interface. The class name is used internally.
Important is, that the name in DOWNLOAD_CLASS_NAME is equal with the used class name.
|
1.3
|
The class from which it is derived, is specified within the brackets after the class name. In this case, it is the base class Downloader.
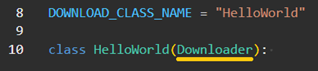

Important: It can only be derived from translators within the installation directory or the current plugin. Taking these conditions into account, several derivations are possible (like described in infrastructure overview picture in the Introduction page).
|
|
|
2
|
Create a program file and add content
|
|
2.1
|
There is a library command available which:
 creates a file if it does not exist. creates a file if it does not exist.
 opens the file. opens the file.
 adds content. adds content.
 closes the file. closes the file.
To access that library, the import of FileUtility from cenpylib is necessary at the beginning of the downloader.

|
2.2
|
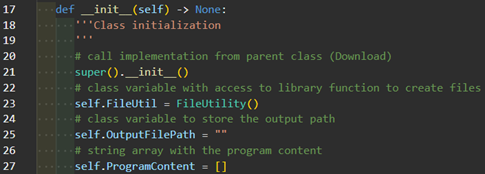
To get access to the library in the entire class, we create class-wide access with self.FileUtil = FileUtility().
This means that the code only must be implemented in the first derivation. The access is then also available in the derived (child) classes (more later).
Do not forget to call the parent implementation of the __init__ function with super().__init__() especially in the child classes.
|
2.3
|
In self.OutputFilePath we will store the output directory, including the file name and the file extension.

|
2.4
|
The string array self.ProgramContent is used to add single lines to that array.

|
2.5
|
At the end, the complete array is transferred to a file using the function AppendTextArrayToFile() from self.FileUtil.

|
|
|
3
|
Get controller information and all connected joints
|
|
3.1
|
Here is an example of how to read the necessary information from the controller and access the axis mapping.
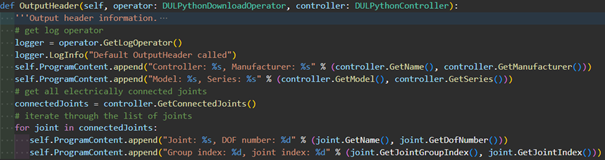
Add the following lines to the OutputHeader() function.
# get log operator
logger = operator.GetLogOperator()
logger.LogInfo("Default OutputHeader called")
self.ProgramContent.append("Controller: %s, Manufacturer: %s" % (controller.GetName(), controller.GetManufacturer()))
self.ProgramContent.append("Model: %s, Series: %s" % (controller.GetModel(), controller.GetSeries()))
# get all electrically connected joints
connectedJoints = controller.GetConnectedJoints()
# iterate through the list of joints
for joint in connectedJoints:
self.ProgramContent.append("Joint: %s, DOF number: %d" % (joint.GetName(), joint.GetDofNumber()))
self.ProgramContent.append("Group index: %d, joint index: %d" % (joint.GetJointGroupIndex(), joint.GetJointIndex()))
|
3.2
|
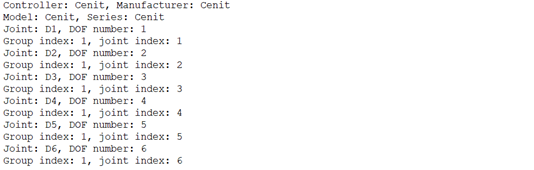
Download the program in your scenario with this update and look for the results.
Example:
|
|
|
4
|
Output all attributes defined on the operation
|
|
4.1
|
To be able to access an attribute in download, the attribute must be of type PROCESS_ATTRIBUTE. It is possible to change the property and visibility of attributes via technology customizing.

|
4.2
|
Output all operation attributes with the property PROCESS_ATTRIBUTE.
Add the following lines to the OperationStart() function.
for att in operation.GetAttributes():
self.ProgramContent.append('Operation attributes: ' + str(att. GetName()) + ',' + str(att.GetValue()))

|
4.3
|
Download the program in your scenario with this update and look for the results.
Example of the output that has been added:
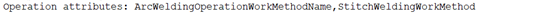
|
4.4
|
In this following example, only attributes that can be found on the operation or have been set on the operation are considered and have the property PROCESS_ATTRIBUTE.
To get a specific process attribute on the operation, the following function should be used.

|
|
|
|
|
5.1
|
The entry to the motions and events is in the function HandleMotion(). First, the events before the movement are processed. Then the movements themselves are translated and finally then the events after the movement.
The example below contains an implementation for point to point, linear and circular motions. In this document we will only describe the linear output.
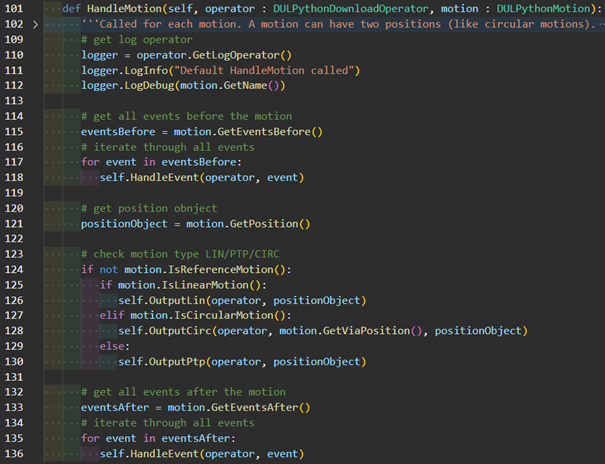
|
5.2
|
Within the OutputLin() function, the string for the output is generated and added to the self.ProgramContent. The output of the self.ProgramContent has already been dealt with in the beginning.
Add the following lines to the OutputLin() function.
# get cartesian coordinates
xyz = position.GetXYZ()
angles = position.GetOrientation()
# convert them to meter
convertToMM = 1000
X = xyz[0] * convertToMM
Y = xyz[1] * convertToMM
Z = xyz[2] * convertToMM
# add motion instruction to the
self.ProgramContent.append(" X:%.3f mm Y:%.3f mm Z:%.3f mm" % (X, Y, Z))
self.ProgramContent.append(" Rx:%.3f deg Ry:%.3f deg Rz:%.3f deg" % (angles[0], angles[1], angles[2]))
self.ProgramContent.append("")

|
5.3
|
Download the program in your scenario with this update and look for the results.
Example:
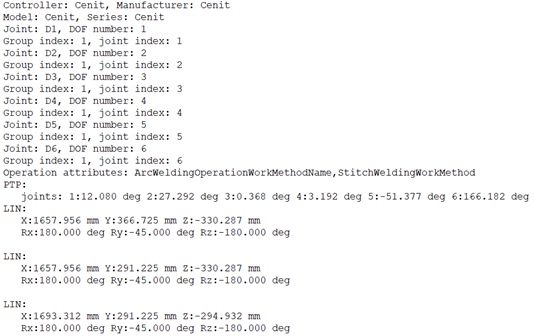
|
|
|
|